


Nachdem gezeigt wurde, dass die tatsächliche Schlüssellänge von der theoretischen Schlüssellänge abweichen kann, stellt sich die
Frage, ob die kürzere Schlüssellänge dennoch als ausreichend betrachtet werden kann um den Datenschutz zu gewährleisten.
Der Datenschutzbeauftragte von Hessen empfiehlt einen 56 Bit langen Schlüssel für den
„Einsatz bei nicht sensiblen personenbezogenen Daten oder in solchen Fällen, in denen ein Angriff mit hohem Aufwand aus anderen
Gründen unwahrscheinlich ist (z. B. geschlossenes Netz). Zukünftige Sicherheitsprobleme sind jedoch zu erwarten“ [DH 2003].
Einen 40 Bit langen Schlüssel hingegen nur als „Schutz gegen zufällige Kenntnisname“ und für den
„Einsatz bei nicht sensiblen personenbezogenen Daten, wenn ein gezielter Angriff unwahrscheinlich ist.“ [DH 2003]
Diese Empfehlung, die auch von anderen Datenschützern und Sicherheitsexperten geteilt wird, bezieht sich jedoch nicht direkt auf den
ePass. Es liegt die Vermutung nahe, dass der Mikroprozessor eines RF-Chips nicht die Leistungsfähigkeit besitzt wie ein
handelsüblicher PC oder ein System, das auf Entschlüsseln spezialisiert ist und somit eine Brute-Force Attacke ungleich länger dauert.
Dennoch haben es Forscher aus den USA geschafft, einen mit 40 Bit verschlüsselten RF-Chip innerhalb einer Stunde zu knacken
[BGSJRS 2005]. Sie vermuten, diese Zeit auf wenige Minuten senken zu können. Der Versuchsaufbau gleicht allerdings nicht der
Situation wie sie beim ePass vorzufinden ist. Zudem müsste sich ein Angreifer für eine ,Live-Brute-Force-Attacke’ permanent in
unmittelbarer Nähe zu dem ePass befinden. Selbst wenn die Chips langfristig um ein Vielfaches leistungsstärker werden und ein Brute
Force Angriff in wenigen Sekunden möglich würde, könnte man diesen leicht unterbinden, indem der Chip erst nach einer kurzen
Verzögerung antwortet. Durch diese Verzögerung würde das Ausprobieren aller möglichen Kombinationen praktisch unmöglich
gemacht, da die Zeitspanne zu groß wäre.
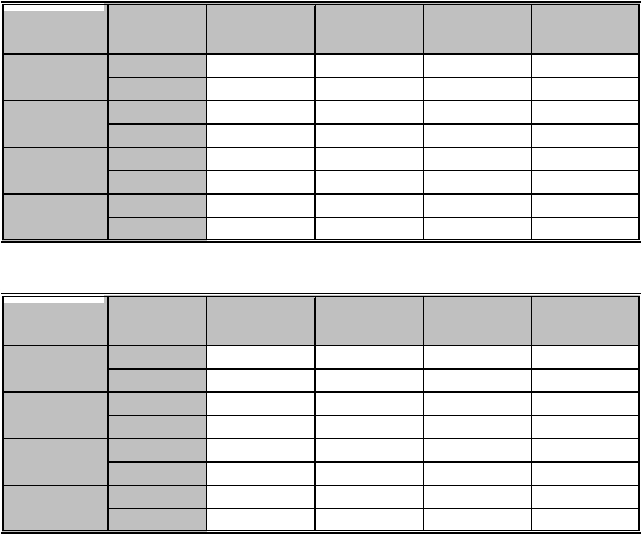
Tabelle 5.5.3a: Tatsächliche Schlüssellänge von Basic Access Control bei 10^9 zufälligen Passnummern [Bit]
Ausstellungs-
tage pro Jahr*
Geburtsdatum
bekannt
Geburtsdatum
geschätzt
(+-5 Jahre)
Geburtsdatum
beschränkt
(16-65 Jahre)
Geburtsdatum
nicht bekannt
(100 Jahre)
365
38
50
53
54
253
38
50
52
53
365
39
51
54
55
253
39
51
53
54
365
41
53
55
56
253
40
52
54
55
365
42
54
56
57
253
41
53
55
56
* 253 Tage pro Jahr unter der Annahme, dass an Wochenenden und Feiertagen keine Pässe ausgestellt werden, 365 sonst
1 Jahr nach
Einführung
2 Jahre nach
Einführung
10 Jahre nach
Einführung
5 Jahre nach
Einführung
Tabelle 5.5.3b: Tatsächliche Schlüssellänge von Basic Access Control bei 10^5 zufälligen Passnummern [Bit]
Ausstellungs-
tage pro Jahr*
Geburtsdatum
bekannt
Geburtsdatum
geschätzt
(+-5 Jahre)
Geburtsdatum
beschränkt
(16-65 Jahre)
Geburtsdatum
nicht bekannt
(100 Jahre)
365
25
37
39
40
253
25
36
39
40
365
26
38
40
41
253
26
37
40
41
365
27
39
42
43
253
27
39
41
42
365
28
40
43
44
253
28
40
42
43
* 253 Tage pro Jahr unter der Annahme, dass an Wochenenden und Feiertagen keine Pässe ausgestellt werden, 365 sonst
1 Jahr nach
Einführung
2 Jahre nach
Einführung
10 Jahre nach
Einführung
5 Jahre nach
Einführung
| Hinweis: Alle Rechte vorbehalten. Eine Verfielfältigung oder Verbreitung dieser Seite oder Teile derselben in elektronischer oder anderer Form ist nicht gestattet. Diese HTML-Version des Buches 'ePass - der neue biometrische Reisepass' ist nicht zum Referenzieren geeignet. Das Buch sowie die PDF Version unterscheiden sich von dieser HTML-Version in Layout und Seitenzahlenangaben. Aufgrund von Konvertierungsschwierigkeiten des Originaldokumentes zu HTML, können auf dieser Seite Datstellungsprobleme auftreten, die in dem Buch und der PDF-Version nicht vorhanden sind. |

